Binary search is a cornerstone of computer science, offering a significant performance improvement over linear search. Among the numerous technical tools available for developers, binary search algorithms are particularly notable for their effectiveness in addressing problems related to sorted data. In this blog, we will delve into the principles of binary search, present practical examples, and examine its applications within data structures, while also evaluating the time complexity of binary search to gain insights into its efficiency.
What is a binary search?
Binary search is an exceptionally efficient algorithm designed to locate an element within a sorted list or array. In contrast to linear search, which examines each element sequentially, a binary search algorithm systematically divides the dataset into two halves, significantly minimizing the number of comparisons required.
The algorithm functions as follows:
- It compares the target value with the middle element of the dataset.
- If the target matches the middle element, the search is declared successful.
- If the target is less than the middle element, the search continues in the left half of the dataset.
- If the target is greater, the search advances to the right half.
This procedure is repeated until the desired element is located or the search space is exhausted.
What are the Examples of Binary Search?
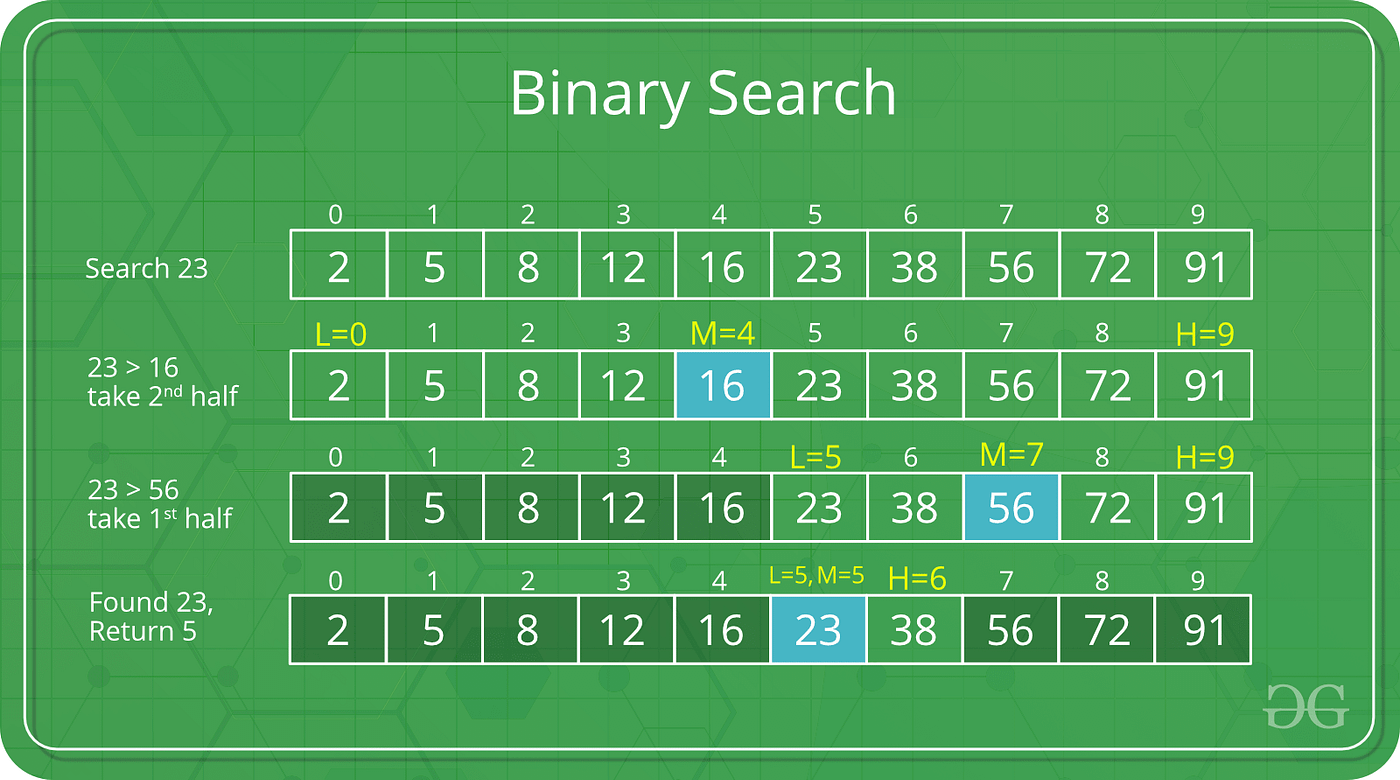
Let’s take a look at one binary search example to better understand its working.
Consider a sorted array: [2, 4, 6, 8, 10, 12, 14], and our objective is to locate the number 10.
First, determine the middle element: (2 + 14) / 2 = 8. The middle value is 8.
Given that 10 is greater than 8, we will concentrate on the right segment: [10, 12, 14].
The new middle element is 12. Since 10 is less than 12, we will now examine the left segment: [10].
The middle value is now 10, which corresponds to our target.
In merely three steps, we successfully identify the target, demonstrating the effectiveness of binary search.
Binary Search in Data Structure
Binary search algorithm plays a crucial role in various data structures and algorithms. Its applications consist of the following:
Arrays and Lists: Binary search is most effective with static datasets where the elements are pre-sorted. In cases of dynamic data, frequent sorting may be necessary, which can reduce its overall efficiency.
Binary Search Trees (BSTs): A BST is a tree-like data structure in which each node can have a maximum of two children. Binary search is fundamental to operations such as insertion, deletion, and searching within BSTs.
Applications in Heaps and Priority Queues: While heaps do not completely support binary search due to their unsorted nature, certain types, such as binary heaps, utilize the concept to enable efficient access to elements.
Advanced Data Structures: Data structures like balanced trees, including AVL and Red-Black trees, apply binary search principles to maintain sorted data and guarantee logarithmic time complexity for various operations.
Time Complexity of Binary Search
One of the primary factors contributing to the widespread use of binary search algorithms is their remarkable time complexity. In a dataset of size n, the algorithm effectively halves the search space with each iteration. As a result, the time complexity of binary search can be written as:
This logarithmic progression indicates that binary search maintains its efficiency even with large datasets. For example:
- In a dataset containing 1,000 elements, binary search allows a maximum of 10 comparisons.
- For a dataset of one million elements, it requires only 20 steps to locate the target.
Best, Worst, and Average Cases
- Best Case: The target is positioned as the middle element, which requires merely one comparison.
- Worst Case: The target is found at either end of the sorted list, demanding more comparisons.
- Average Case: On average, binary search operates in O(log n), establishing it as a reliable option.
What are the Benefits of Binary Search
There are many benefits of the binary search algorithm which are as follows:
- Efficiency: The logarithmic time complexity of this algorithm guarantees swift search operations, rendering it suitable for extensive datasets.
- Simplicity: The clear and uncomplicated logic of the algorithm facilitates both implementation and comprehension.
- Versatility: Binary search is applicable in numerous fields, such as databases, operating systems, and computational biology.
- Memory Efficiency: The algorithm operates in place, eliminating the need for extra storage during the search process.
Real-World Applications of Binary Search
There are multiple real-world applications of the binary search algorithm which are as follows:
- Databases: The principles of binary search form the foundation for indexing structures such as B-trees and hash indexes.
- Gaming: In computer graphics, binary space partitioning (BSP) algorithms, which are based on binary search concepts, are used to efficiently render 3D scenes.
- Search Engines: The efficiency of locating keywords within sorted datasets is enhanced by the application of binary search.
- Finance: In the analysis and forecasting of stock market trends, binary search is employed to manage extensive datasets of historical price information.
Conclusion
Binary search algorithms showcase the effectiveness of efficient problem-solving within the realm of computer science. Utilizing the divide-and-conquer approach, these algorithms enable swift searching in sorted datasets, serving as a fundamental component in various applications related to data structures and practical systems. The straightforward nature of the binary search example, coupled with its crucial function in data structures, underscores the algorithm’s importance. With a time complexity that prevails over many other methods, proficiency in this algorithm is vital for any aspiring programmer or data scientist.
Whether you are developing basic search features or architecting complex systems, binary search stands as a pillar of computational efficiency. Recognize its potential and use it to achieve the best possible results.
 Join Daily Trust WhatsApp Community For Quick Access To News and Happenings Around You.
Join Daily Trust WhatsApp Community For Quick Access To News and Happenings Around You.